A Story about Hash Functions
H: M → T, where |M| >> |T|
November 2018
Hash functions are fundamental to the operation of a blockchain system. Most everybody knows what they are used for and has a basic understanding of their properties. This article is for the curious minds that want to take a peek under the hood and see the hamsters spinning the wheels.
Say we ask a random crypto-hodler about hash functions. The answers would be along these lines:
- hash functions take arbitrarily long messages and output a fixed-length value, called digest;
- it is practically impossible to calculate the input from the output, but very easy to do the inverse;
- different inputs produce different outputs.
Such characteristics are very useful in the realm of digital signatures, data integrity and authentication verification, key derivation, etc., but the general public got to know them with the emergence of digital currencies and blockchain networks. Mention SHA-256 to any Bitcoin aficionado or Keccak-256 to a proud cryptokitty owner and observe the shine in their eyes. Yet we often treat hash functions as pure magic, confusing them with encryption or, worse, consider them a priori secure and impenetrable. Here’s to hoping that uncovering a bit of mystery around them will help appreciate them more.
H is hash function that transforms a message m from a large space M to a tag t from a much smaller space T.
H: M → T, where |M| >> |T|
Generally, hash functions compress data to its shorter representation. Let’s say we have strings "aabbcc", "bbccdd", "ccddee" ... A simple hash function would map them to "a", "b" and "c" ... thus "a" is an image of "aabbcc". Following this naive algorithm, once we add an input string "ababab" and map it to “a”, we immediately see the problem. We don’t know what "a" represents, we don’t know how to address "aabbcc" anymore, and we are not sure if increasing the digest length would help (say by mapping inputs to their first two letters, "aabbcc" → "aa" and "ababab" → "ab"), or would it just prolong the pain.
To make more sense, we define secure cryptographic hash functions with two (simplified) properties.
1. They are one-way only, meaning that we can’t compute the input from the output, a.k.a. preimage resistance. Given “a”, we indeed cannot deduct whether it represents “aabbcc” or “ababab” or whatever.
2. It is hard to find two different inputs which would have the same digest value, a.k.a. collision-resistance. Given “a”, it can only represent “aabbcc” or “ababab”, exclusively.
Collision is when different messages produce the same tag. Since |T| is much smaller then |M|, there are going to be many collisions. We can imagine hash functions to be surjective (each value in the range is a transform of at least one value in the domain), though take it lightly as I’m not sure if it can be proven or if proving it wouldn’t negatively affect their security. We want such H, that collisions explicitly don’t happen.
In essence, we have a 3-step challenge: how to accept lengthy inputs, how to avoid collisions, and how to make it one-way.
As a first step, let’s assume we already have a collision-resistant hash function that accepts single-length input and computes its image with the two previously mentioned properties. Now, we have to create a system that preserves the security but works with inputs of any length. Which is where Merkle-Damgård construction comes to help, published in 1979 by Ralph Merkle (though discovered in 1974 – read the sad story of publishing such novel ideas: http://www.merkle.com/1974/) and Ivan Damgård (who interestingly doesn’t even seem to list his independent discovery from 1987, published in 1989, on his website: http://www.daimi.au.dk/%7Eivan/papers.html).
Merkle-Damgård construction works by breaking a large input message m into smaller blocks (m = m[0] || m[1] || ... m[k]) and in iterative steps apply compression function h on two inputs: the current message block m[i] and the previous output Hi, also called a chaining variable. Blockchain much. Since the first h doesn’t have an input from previous block, a standardized initialization vector IV is used. In the same fashion, since the last block might not be full (m mod |m[i]| ≥ 0), a padding block PB is added, where PB must end with 64-bit description of message m's size. Side note: inputs are thus limited to 264 -1 bits, which is sufficient for practical use (~ 1019 or 10 exabits).

It is provable that if the compression function h is collision-resistant, then hash function H is as well.
Secondly, how to construct h that is collision-resistant ? A common way is using Davies-Meyer construction: Hi = E (mi, Hi-1) XOR Hi-1
A fascinating twist is the use of block ciphers E: K x {0,1}n → {0,1}n, which encrypt n-bits using a key from K to an n-bit long cipher text. Thus, in hash functions, there could be some encryption as well! Besides block ciphers, there are other methods, but tend to be slower. Using E we get secure transformation (indistinguishable from random output) and adding the XOR the computation is un-invertable, precisely what we needed.

It is provable that this is as collision-resistant as possible and Davies-Meyer compression function is therefore standard nowadays, though there are others (e.g. Matyas-Meyer-Oseas, Miyaguchi-Preneel ...) following a similar idea. DM has a side twist on its own: Preneel, Govaerts and Vandewalle presented a general model of all possible schemes in 1994, referencing DM as well, but actually Donald Davies denied contributing to the scheme, so it might be named after him just to be in his honour (see: Hash functions based on block ciphers: a synthetic approach, 1993). Humans.
MD-DM constructions could provide quantum security as well, supposedly with minor changes in rules and parameters (see https://eprint.iacr.org/2018/841.pdf).
Finally, what could E be in the specific use of hashing? That’s the core of it and thus varies from one hash function to another. Starting with DES (1977), but modern designs really expand work on much faster MD5 (Rivest, 1992) (see: The First 30 Years of Cryptographic Hash Functions and the NIST SHA-3 Competition, 2010). The essence of MD5 is: a 128-bit state, four 32-bit initial constants A, B, C, D, 512-bit message blocks which are processed in 4 different stages (rounds) of 16 operations each, consisting of bit rotations, modular addition and funky functions on ABCD. After each of 64 operations, the state is updated until its final addition to the initial constants.
SHA-0 follows similar principle, as is slightly modified but much more secure SHA-1, which is based on SHACAL block cipher (Handschuh and Naccache, 2000). However when AES was published (2001), new hash functions were needed as well, thus SHA-2 family was introduced (2002), with three functions: SHA-256, SHA-384, SHA-512.
The world-wide popular SHA-256, that is mentioned in every other article about Bitcoin, still uses MD construction with DM compression function, with SHACAL-2 block cipher. SHACAL-2 uses 512-bit message blocks as key, thus SHA-256 processes 512-bits at a time with 256-bit chaining variables, as shown on the image below. SHACAL-2 uses twice the number of state bits, so IV is eight 32-bit registers, which get updated throughout all 64 rounds. SHACAL-2 is considered secure as of 2018, it was included in the project New European Schemes for Signatures, Integrity and Encryption in 2003. The current best attack is on 44 rounds (Lu & Kim, 2008).

SHA-3 family is the latest in NIST standards (2015), that takes a different design: there are significant changes in its internal mode of operation, enabling variable-length outputs using sponge constructions (see https://keccak.team/sponge_duplex.html). SHA-3 is a subset of Keccak family. While Bitcoin heavily relies on SHA-2, Ethereum is using SHA3 instead. The goal was to try to use an even more secure hashing function (this was happening right in the midst of the revelations of Edward Snowden, thus Ethereum (a.k.a. web3) was referred as “post-Snowden Web”), but SHA-3 wasn’t yet standardized at that time, NIST standard was finalized only in August 2015. Ethereum therefore used a version called Keccak-256, and since the standardized SHA3 actually changed a bit since then, we receive different results if we compare SHA-3 from NIST and SHA-3 used in Ethereum. Therefore, when using a hashing function in Ethereum, it would be best not to use sha3(), but to use its alias keccak256(). That would be more correct and less ambiguous.
Keccak family was an evolution on work from 2008, though its origin go even further back, to 1998 and the PANAMA algorithm. Giving it roughly 15 years of scrutinized critics before accepting a secure version of it. Be wary of hash functions made in a garage, they are rather ridiculous.
References:
- Bitcoin and Cryptocurrency Technologies by Arvind Narayanan, Joseph Bonneau, Edward Felten, Andrew Miller, Steven Goldfeder, available online as well (at least the draft from 2016).
- Cryptography course by Dan Boneh on Coursera is great.
- Handbook of Applied Cryptography by A. Menezes, P. van Oorschot, and S. Vanstone (2001), chapters available online.
G
...
A side note, for which I hope to have more time to delve deeper in the future ...
Say we want to make sure a message wasn’t tampered with, we want to be sure that its integrity is intact. With a collision resistant hash function, A can send a message m with digest t to the recipient B and he/she can quickly re-calculate the digest from that message to be sure they match. However if an attacker forges the message with m’ and provides its t’, B will not detect any problem. Thus, message authentication requires a shared key in the computation (MAC, message authentication code). Having A and B share a secret key k, the attacker won’t be able to forge the proof digest – that is a secure MAC.
MAC {S, V}: signing algorithm S (k, m) = t, verification algorithm V (k, m, t) = true/false
MAC is secure, if S is secure PRF: K x X → Y, where the output range is large: |Y| >> 280. Meaning that the attacker has only brute force guessing at hand and it is practically impossible to forge.
Next, it would be nice to be able to use MAC with messages of any lengths - hash-based MACs (HMAC) work on hashes of messages, instead of on messages directly. Meaning that they can be applied to large inputs, providing that the hash function is secure (collision resistant). HMAC-SHA512 is used in Bitcoin for key derivation.
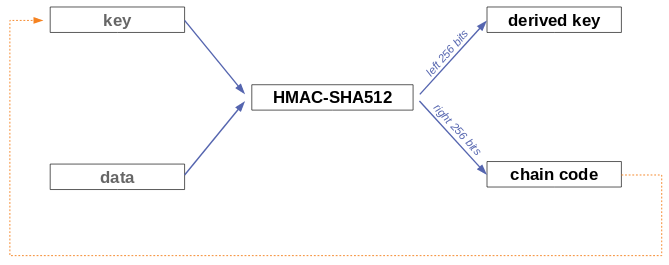
Integrity could be proven with collision resistant hashing without sharing a secret key by comparing inputs to known hash digests – but this known digests would need to be read-only, otherwise an attacker could simply alter them to match his forged inputs. Thus, this read-only property is critical. → digital signatures !!!